Nonlinear and chaotic dynamical systems are unpredictable even without random perturbations that are inherent in nature. To-date, complex spatio-temporal, self-modulated, non-stationary or chaotic responses that cannot be explained by standard linear analysis, are typically obtained from either elaborate theoretical nonlinear continuum models, or from simplistic nonlinear lumped-mass models. While continuum models can be integrated numerically, they are still computationally expensive and do not readily enable mapping of all multiple coexisting stable, and more importantly, cannot determine unstable solutions that govern the stable response basins of attraction. Furthermore, while lumped-mass models can sometimes be approximated analytically, they do not accurately account for dispersion, multimode coupling or the true nonlinear nature of coupled-space time. An alternative to these two modeling approaches is that of nonlinear continuum-based reduced-order models. This approach enables application of a consistent methodology for incorporation of governing nonlinear effects in a tractable mathematical model that captures the essential spatio-temporal dynamics, and its outcome can yield an accurate system response bifurcation structure asymptotically and numerically.
Within the broad range of nonlinear continuum-based reduced-order models, the focus of the Gottlieb Group is on two main areas: (A) nonlinear continuum mechanical systems, and (B) nonlinear fluid-structure interaction. In both areas, We make use of a combinedasymptotic and numerical bifurcation methodology to investigate nonlinear interactions and employ chaos theory to determine the global nature of instabilities that are governed by sensitivity-to-initial-conditions. In what follows is a description of our main contributions in each area.
(A1) Dynamics of scanning probe microscopes
We have derived and analyzed a continuum based model for a smart piezoelectric micro-cantilever [WG-2002] for non-contacting atomic force microscopy (AFM). It is noteworthy that this model and its nonlinear asymptotic analysis were later independently validated experimentally (Usher and Sim, J. Appl. Phys., 2005). This research was extended to account for nonlinear dissipation measured experimentally [GWHME-2007] and for coupled mode operation in high vacuum [GWHS-2012].To date, the majority of existing models consist of lumped-mass formulations that do not enable consistent derivation of multi-mode dynamics that is required for simultaneous imaging and force-detection. Consequently, the significance of this work is that it accurately incorporates the continuum effects including piezoelectric actuation (via Hamilton’s principle) and atomic interaction as a nonlinear boundary condition [WG-2002], or as a localized force that has been recently implemented for control of the scan process [HG-2008]. The localized force model has further enabled derivation of global (Melinkovbased) theoretical bound for robust control that avoids the critical ‘jump-to-contact instability’ that occurs during the scan process when the atomic attraction is greater than the elastic restoring force, consequently causing the sensing tip to crash and possibly stick to the sampled substrate [HG-2012].
A spatio-temporal model derivation of a noncontact AFM with external feedback control [SGR-2015] has shown that a combined asymptotic and numerical bifurcation analysis enables identification of stability threshold required of robust controllable operation.
The methodology derived for the AFM scan process, is currently implemented (via ISF and RBNI-CFN grants) for novel hybrid elements designed for simultaneous internal-resonance based multiple-sensing applications [HSG-2012], and is adapted to magnetic resonance force microscopy (MRFM) that can identify electron spin changes [GHR-2012].
A recent combined aymptotic and numerical analysis has shown that a vertical configuration requires implementation of a reconstitution multiple-scales to yield an accurate form of the system evolution equations [GH-2019] and that combined local and global bifurcation analysis is essential to resolve the response domains of attraction of a horizontal configuration [GH-2020].
(A2) Loss of synchronization in micro-resonator arrays
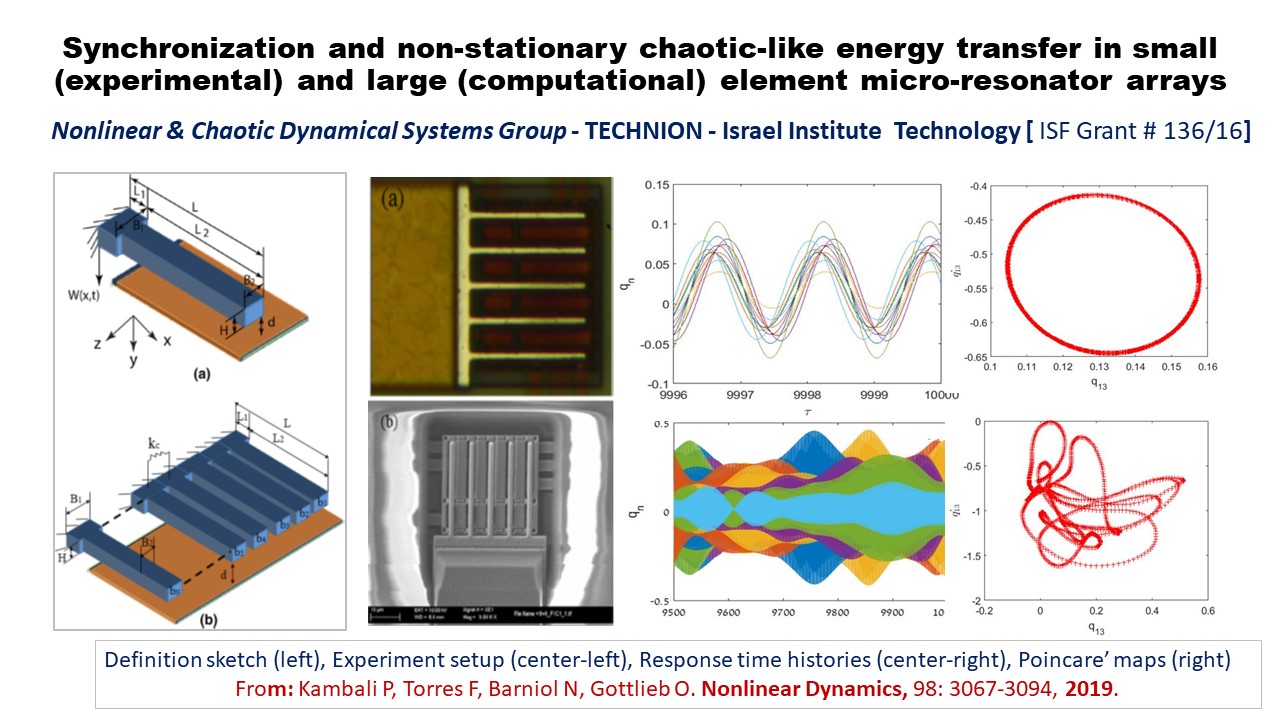In a series of papers [GG-2010,2012] we have formulated and analyzed an initial-boundary-value-problem which includes a small size array of microbeams that are subject to parametric electro-dynamic actuation. Multiple element arrays appear in a variety of applications such as mass detection, signal-mixing and parallel lithography. However, to-date, the research has been experimental, complemented by computer intensive finite element models and simplistic lumped mass models. The former are useful in identification of linear resonances whereas the latter only predict existence of synchronized periodic solutions. The recent research analytically demonstrates that excitation at low, medium and large DC voltage generates non-negligible internal and combination resonances that govern the onset of quasiperiodic and chaotic dynamics. The crucial difficulty in problems with parametric excitation is the estimation of nonlinear damping, without which mathematical solutions grow-without-bound. Motivated by experimental evidence that system dissipation increases with input voltage, we have proposed [GG-2010] a novel Rayleigh based nonlinear dissipation mechanism that mimics the electro-dynamic excitation, and successfully augments the array element visco-elastic dissipation. The theoretical predictions enabled by this research program are currently being implemented experimentally (via a BNCN-RBNI grant) for the design of smart sensor arrays for multi-functional detection by micro- and nano-scale elements that can be excited by combined direct and parametric excitation.
A recent computational analysis [KTBG-2019] demonstrates the possible nonstationary chaotic-like energy transfer in a large micro-cantilever array with 25 coupled elements.
(A3) Chaotic thermo-visco-elastic nano-resonators
We formulate and investigate quasi-continuum models for thermo-visco-elastic micro- and nano-resonators that are excited via electrodynamic [GC-2005], electromagnetic [WSGHR-2012], or optical modulation [ZGB-2012]. Analysis of these models is essential for prediction of resonator dynamics operating in high vacuum where non-stationary thermal noise can mask the fundamental electromechanical response, and thus prevent optimal sensing. This research includes both micro- [ZBSG-2012] and nano- [GGB-2007] mechanical oscillators governed by linear and nonlinear visco-elastic damping mechanisms where thermal effects are negligible, and resonators and cantilever sensors that require simultaneous modeling and analysis of coupled elastic and thermal fields. While the former reveal coexistence of bi-stable solutions [ZSBG-2012] and a complex quasi-periodic bifurcation structure [GGB-2007] due to external excitation, the latter reveal homoclinic bifurcations [GC-2005] and self-modulation culminating with chaotic strange attractors [HG-2012] due to laser irradiation of the integrated optical sensor vibrometers. The nonlinear continuum based reduced order models are validated via experimental data and enables a consistent explanation of chaotic energy transfer between the resonator response modes that is not possible via a lumped-mass approach.
(B1) Non-stationary travelling waves
Nonlinear waves in continuum domains, include open questions regarding the mechanisms governing the resulting spatio-temporal complexity. An example where a low-order analytical nonlinear dynamical system approach reveals the complete bifurcation structure that is unattainable via experiments or using expensive numerical analysis is that of falling thin film dynamics. We were able to demonstrated for the first time that the irregular bifurcation structure which was previously thought to be non-stationary from numerical analysis [GO-2004], is actually quasi-periodic, and as such is predictable. This result sheds light on the mechanism governing the evolution of complex non-stationary wave patterns that emerge as an outcome of harmonic perturbation of the thin film boundary. Similar behavior has been documented in biological applications and can possibly account for the unsteady dynamics measured in thyroid patients [GCCI-2011] via the orbital loss of stability of a steady solution in a calibrated eight-order model.
An additional bio-inspired example motivated by the onset of the yet unexplained spontaneous oto-acoustic emissions that emerge from the cochlea in the inner ear, is the analysis of a nonlinear string on an elastic foundation subject to a nonlinear feed-forward force that represents the self-modulated fluid-structure interaction of the hair-cells with the Basilar membrane [GC-2010]. In this research, we have demonstrated for the first time analytically and numerically that quasi-periodic combination tones and non-stationary dynamics occur below primary and secondary bifurcation thresholds, respectively.
(B2) Wave-structure interaction
Externally excited fluid-structure interaction systems in severe environmental conditions exhibit multiple coexisting solutions culminating with non-stationary response which precedes structural failure. Examples are a rigid-body ship in finite amplitude head seas [KG-2009] and acoustically excited panels in air [AG-2012] which can capsize or fail due to sonic fatigue respectively. Thus, it is crucial to understand the finite amplitude structural response prior to failure in order to avoid or suppress it. The Gottlieb group has been able to implement a combined asymptotic and numerical bifurcation methodology that sheds light on energy transfer between critical modes via both internal and combination resonances. A nonlinear dynamical system model for ship dynamics in periodic head seas was analyzed and compared to experimental measurements of a small fishing vessel, whereas a continuum nonlinear elastic panel model in an Euler field subject to acoustic fluid-structure interaction was analyzed and compared to a benchmark NASA experiment (Maestrello et al, AIAA Journal 30, 1992) where non-stationary panel response was estimated as chaotic. The results of both investigations revealed the crucial importance of nonlinear dissipation demonstrating that nonlinear damping governs the response bifurcation structure for both parametrically excited ship dynamics [KG-2012] and externally excited panels [AG-2012]. Furthermore, the combined asymptotic and global rigid-body analysis has recently enabled derivation of a novel design threshold for ships in head seas [KG-2011], whereas the onset of chaotic panel response to harmonic excitation reveals that the intricate pattern formation of the radiated near pressure field is an outcome of an ultra-sub-harmonic crisis [AG-2010].
(B3) Vortex-induced vibration
Vortex-induced vibration (VIV) of rigid-bodies in steady flow is a fundamental nonlinear phenomena governed by a (Hopf) stability threshold beyond which the fluid-structure interaction becomes either periodic, quasiperiodic or non-stationary. We have recently proposed and validated a consistent methodology for a multiple-scale asymptotic model-based estimation procedure which enables prediction of the chaotic and non-stationary response documented for elastically tethered rigid-bodies [GDG-2010] and three-dimensional phenomena in both light and heavy tethered spheres [SG-2012]. We note that to-date, theoretical estimation of the VIV bifurcation structure is limited to prediction of periodic (lock-in) response, whereas the combined asymptotic and numerical analysis enables identification of secondary bifurcation thresholds that have been validated experimentally [HKG-2010] and numerically [DDG-2012]. It is noteworthy that a Lagrangian based model derived for a nonlinear spherical pendulum [GH-2012] augmented by a wake oscillator accurately predicts the periodic self-excited dynamics described by benchmark experiments in literature, and reveals the existence of an orbital stability threshold [SG-2012] that is not readily predicted by computational fluid dynamics. The current efforts of the Gottlieb group are focused on numerical validation and implementation of the asymptotic coupled wake-structure models to stabilization of restrained lighter-than-air-systems (LTAS) in severe environmental conditions. The current efforts of the Gottlieb group are focused on numerical validation and implementation of the asymptotic coupled wake-structure models [MG-2015, 2016] to stabilization of restrained lighter-than-air-systems (LTAS) in severe environmental conditions [MG-2017,2018].
(B4) Identification of nonlinear damping mechanisms
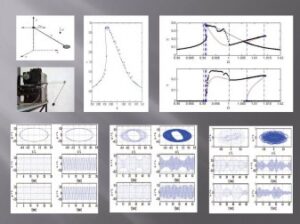An understanding of nonlinear dissipation mechanisms in engineeirng systems is of particular imortance in processes governed by self-excited modulation, external and parametric excitation. Without such an intimate knowledge solution topology and stability thresholds can be inaccurate, and response may spuriously grow without bound. Examples include chaotic fluid-structure-interaction where there exists discrepancies between measurements and theoretical results obtained from nonlinear models with linear damping. We consider the chaotic spherical pendulum under horizontal base excitantion where in order to accurately model the effects of nonlinear damping, we employ a spline-based methodology where controlled measurements of motion in both air or water are decomposed into slowly-varying amplitude and phase, which in-turn enable construction of nonlinear frequency and damping backbone curves. The latter enable estimation of nonlinear damping mechanisms in models that can be reduced to their equivalent normal forms by temporal multiple-scale asymptotics. Validation of the nonlinear model-based damping mechanism is obtained by comparison to independently obtained data.
(B5) Flow-induced oscillation
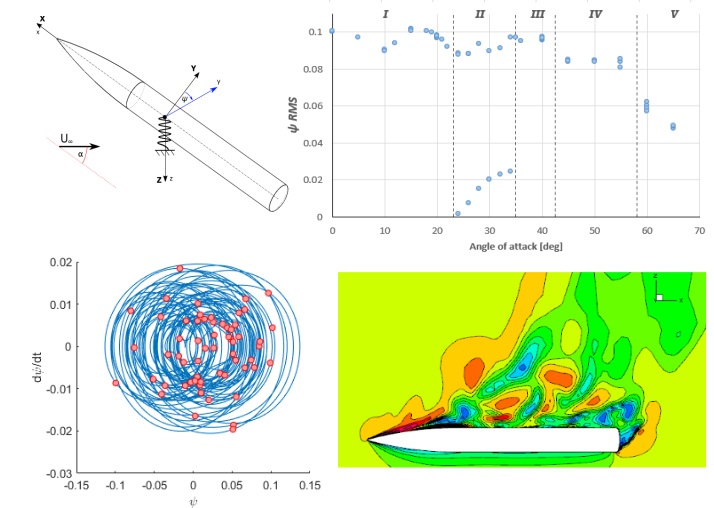One of the most crucial phenomena associated with FSI is flow-induced oscillation, which is the periodic and non-stationary oscillatory response of a coupled fluid–structure system due to fluid forcing. The self-excited response of an elastically restrained inclined tangent ogive-cylindrical body with a blunt elliptical base is investigated numerically [GGD-2015, KGDG-2016]. The flow is three-dimensional, compressible, and laminar and the slender body can roll [DIG-2017] or yaw [IGD-2021] at high incidence. The resulting response exhibits an intricate bifurcation structure that includes bi-stable periodic (finite amplitude) and non-stationary (small amplitude) limit cycles for moderate angles of attack, and non-stationary (finite amplitude) oscillations for high angles of attack.